A. Phương pháp giải & Ví dụ
Phương pháp giải
1. Định nghĩa: Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.
Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
2. Điều kiện cần để hàm số đơn điệu: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0,∀x ∈ K và f'(x) = 0 xảy ra tại một số điểm hữu hạn.
Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0,∀x ∈ K và f'(x) = 0 xảy ra tại một số điểm hữu hạn.
3. Điều kiện đủ để hàm số đơn điệu: Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
Nếu f'(x) > 0,∀x ∈ K thì hàm số đồng biến trên khoảng K.
Nếu f'(x) < 0,∀x ∈ K thì hàm số nghịch biến trên khoảng K.
Nếu f'(x) = 0,∀x ∈ K thì hàm số không đổi trên khoảng K.
4. Các bước xét tính đơn điệu của một hàm số cho trước
Bước 1: Tìm tập xác định của hàm số y = f(x)
Bước 2: Tính đạo hàm f'(x) và tìm các điểm xo sao cho f'(xo) = 0 hoặc f'(xo) không xác định.
Bước 3: Lập bảng xét dấu và đưa ra kết luận
Ví dụ minh họa
Ví dụ 1: Xét tính đồng biến và nghịch biến của hàm số sau y=x3 - 6x2 + 9x -3
Hướng dẫn
Tập xác định: D = R
Ta có y' = 3x2 - 12x + 9
y' = 0 ⇔
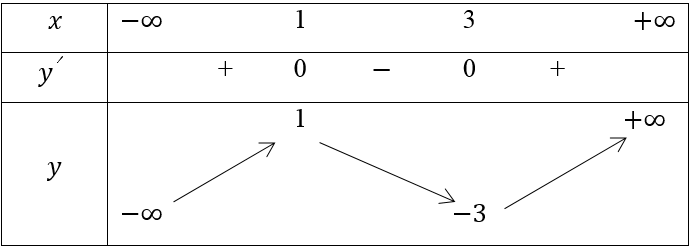
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng (-∞;1) và (3;+∞)
Hàm số nghịch biến trên khoảng (1;3)
Ví dụ 2: Xét tính đồng biến và nghịch biến của hàm số sau √(2x-x2)
Hướng dẫn
Tập xác định D = [0; 2]
Ta có : y' = 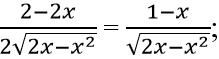
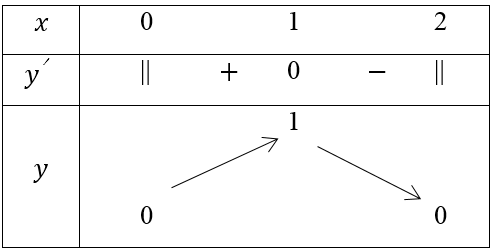
Bảng biến thiên
Vậy hàm số đồng biến trên khoảng (0; 1); Hàm số nghịch biến trên khoảng (1; 2)
Ví dụ 3: Xét tính đồng biến và nghịch biến của hàm số sau y = (3x + 1)/(1 - x)
Hướng dẫn
Hàm số xác định và liên tục trên D = R\{1}.
Tìm y' = 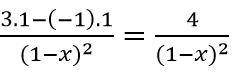
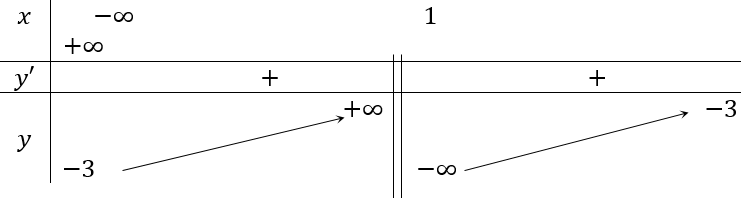
Bảng biến thiên:
Hàm số đã cho đồng biến trên các khoảng (-∞ ; 1)và (1 ; +∞).
B. Bài tập vận dụng
Bài 1: Xét tính đồng biến và nghịch biến của hàm số sau y = y= -x3 + 6x2 - 9x + 4
Bài 2: Xét tính đồng biến và nghịch biến của hàm số sau y = (3 - 2x)/(x + 7)
Bài 3: Xét tính đồng biến và nghịch biến của hàm số sau y = x4 + 4x + 6
Bài 4: Xét tính đồng biến và nghịch biến của hàm số sau y =
Bài 5: Xét tính đồng biến và nghịch biến của hàm số sau y =
Bài 6: Xét tính đồng biến và nghịch biến của hàm số sau y =
Bài 7: Xét tính đồng biến và nghịch biến của hàm số sau y = |x2 - 2x - 3|
Bài 8: Xét tính đồng biến và nghịch biến của hàm số sau y = 2sinx + cos2x,x ∈ [0; π]

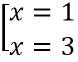
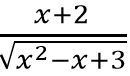
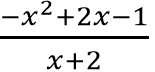

.jpg)
.jpg)

