Lý thuyết tổng hợp chương Mệnh đề, Tập hợp

MỆNH ĐỀ

1. MỆNH ĐỀ

Mỗi mệnh đề phải đúng hoặc sai.

Mỗi mệnh đề không thể vừa đúng, vừa sai.

2. PHỦ ĐỊNH CỦA MỘT MỆNH ĐỀ

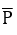
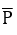
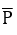
Kí hiệu mệnh phủ định của mệnh đề P là  ta có

 đúng khi P sai.

 sai khi P đúng.

3. MỆNH ĐỀ KÉO THEO

Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, và kí hiệu là P => Q.

Mệnh đề P => Q còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.

Mệnh đề P => Q chỉ sai khi P đúng và Q sai.

Như vậy, ta chỉ xét tính đúng sai của mệnh đề P => Q khi P đúng. Khi đó, nếu Q đúng thì P => Q đúng, nếu Q sai thì P => Q sai.

Các định lí, toán học là những mệnh đề đúng và thường có dạng P => Q.

Khi đó ta nói P là giả thiết, Q là kết luận của định lí, hoặc P là điều kiện đủ để có Q hoặc Q là điều kiện cần để có P.

4. MỆNH ĐỀ ĐẢO – HAI MỆNH ĐỀ TƯƠNG ĐƯƠNG

Mệnh đề Q => P được gọi là mệnh đề đảo của mệnh đề P => Q

Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.

Nếu cả hai mệnh đề P => Q và Q => P đều đúng ta nói P và Q là hai mệnh đề tương đương. Khi đó ta có kí hiệu P <=> Q và đọc là tương đương, hoặc là điều kiện cần và , hoặc khi và chỉ khi.

5. KÍ HIỆU ∀ VÀ ∃

Kí hiệu ∀ đọc là với mọi.

Kí hiệu ∃ đọc là có một (tồn tại một) hay có ít nhất một(tồn tại ít nhất một).

Phủ định của mệnh đề “ ” là mệnh đề “”

Phủ định của mệnh đề “ ” là mệnh đề “”

TẬP HỢP VÀ CÁC PHÉP TOÁN TẬP HỢP

1. Tập hợp

•Tập hợp: là một khái niệm cơ bản của toán học, không định nghĩa.

•Cách xác định tập hợp:

+ Liệt kê các phần tử: viết các phần tử của tập hợp trong hai dấu móc { … }.

+ Chỉ ra tính chất đăc trưng cho các phần tử của tập hợp.

•Tập rỗng: là tập hợp không chứa phần tử nào, kí hiệu ∅.

2. Tập hợp con – Tập hợp bằng nhau

• A B <=> (∀x ∈ A => x ∈ B)

Các tính chất:

+ A ⊂ A, ∀A + ∅ A, ∀A + A ⊂ B, B ⊂ C => A ⊂ C

• A = B <=> (A ⊂ B và B ⊂ A) <=> (∀x; x ∈ A <=> x ∈ B)

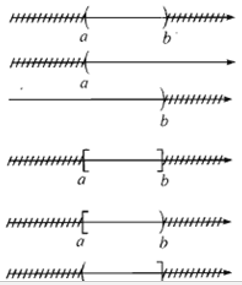
3. Một số tập con của tập hợp số thực

Khoảng

(a; b) = {x ∈R| a < x < b}

(a; +∞) = {x ∈R| a < x}

(–∞; b) = {x ∈R| x < b}

Đoạn

[a; b] = {x ∈R| a ≤ x ≤ b}

Nửa khoảng

[a; b) = {x ∈R| a ≤ x < b}

(a; b] = {x ∈R| a < x ≤ b}

[a; +∞) = {x ∈R| a ≤ x}

(–∞; b] = {x ∈R| x ≤ b}

4. Các phép toán tập hợp

• Giao của hai tập hợp: A ∩ B <=> {x| x ∈ A; x ∈ B}

• Hợp của hai tập hợp: A ∪ B <=> {x| x ∈ A hoặc x ∈ B}

• Hiệu của hai tập hợp: A \ B <=> {x| x ∈ A và x ∈ B}

Phần bù: Cho B A thì CAB = A \ B.

SỐ GẦN ĐÚNG VÀ SAI SỐ

1. Ôn tập quy tắc làm tròn số

Trong sách giáo khoa Toán 7 tập một ta đã biết quy tắc làm tròn đến một hàng nào đó (gọi là hàng quy tròn) như sau

Nếu chữ số sau hàng quy tròn nhỏ hơn thì ta thay nó và các chữ số bên phải nó bởi chữ số

Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng thì ta cũng làm như trên, nhưng cộng thêm một đơn vị vào chữ số hàng quy tròn.

2. Cách viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước

Ví dụ 2. Cho số gần đúng a = 2 841 275 có độ chính xác d = 300. Hãy viết số quy tròn của số a.

Giải.

Vì độ chính xác đến hàng trăm (d = 300) nên ta quy tròn a đến hàng nghìn theo quy tắc làm tròn ở trên.

Vậy số quy tròn của a là 2 841 000.

Ví dụ 3. Hãy viết số quy tròn của số gần đúng a = 3,1463 biết: 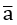 = 3,1463 ± 0,001

Giải.

Vì độ chính xác đến hàng phần nghìn (độ chính xác là 0,001) nên ta quy tròn số 3,1463 đến hàng trăm theo quy tắc làm tròn ở trên. Vậy số quy tròn của a là 3,15.