Lý thuyết: Số gần đúng. Sai số

I. SỐ GẦN ĐÚNG

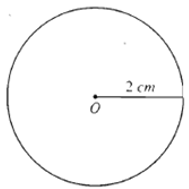
Ví dụ 1. Khi tính diện tích của hình tròn bán kính r = 2 cm theo công thức S = π.r2.

Nam lấy một giá trị gần đúng của π là 3,1

và được kết quả S = 3,1.4 = 12,4 cm2

Minh lấy một giá trị gần đúng của π là 3,14

và được kết quả S = 3,14.4 = 12,56 cm2

Vì π = 3,14592653… là một số thập phân vô hạn không tuần hoàn, nên ta chỉ viết được gần đúng kết quả phép tính π.r2 bằng một số thập phân hữu hạn.

II. QUY TRÒN SỐ GẦN ĐÚNG

1. Ôn tập quy tắc làm tròn số

Trong sách giáo khoa Toán 7 tập một ta đã biết quy tắc làm tròn đến một hàng nào đó (gọi là hàng quy tròn) như sau

Nếu chữ số sau hàng quy tròn nhỏ hơn 5 thì ta thay nó và các chữ số bên phải nó bởi chữ số 0.

Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên, nhưng cộng thêm một đơn vị vào chữ số hàng quy tròn.

Chẳng hạn

Số quy tròn đến hàng nghìn của x = 2 841 675 là x ≈ 2 842 000 của y = 432 415 là y ≈ 432 000

Số quy tròn đến hàng trăm của x = 12,4253 là x ≈ 12,43, của y = 4,1521 là y ≈ 4,15 .

2. Cách viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước

Ví dụ 2. Cho số gần đúng a = 2 841 275 có độ chính xác d = 300. Hãy viết số quy tròn của số a.

Giải.

Vì độ chính xác đến hàng trăm (d = 300) nên ta quy tròn a đến hàng nghìn theo quy tắc làm tròn ở trên.

Vậy số quy tròn của a là 2 841 000.

Ví dụ 3. Hãy viết số quy tròn của số gần đúng a = 3,1463 biết: 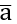 = 3,1463 ± 0,001

Giải.

Vì độ chính xác đến hàng phần nghìn (độ chính xác là 0,001) nên ta quy tròn số 3,1463 đến hàng trăm theo quy tắc làm tròn ở trên. Vậy số quy tròn của a là 3,15.