Lý thuyết: Mệnh đề
I. MỆNH ĐỀ
Mỗi mệnh đề phải đúng hoặc sai.
Mỗi mệnh đề không thể vừa đúng, vừa sai.
II. PHỦ ĐỊNH CỦA MỘT MỆNH ĐỀ
Kí hiệu mệnh phủ định của mệnh đề P là 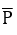
- 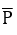
- 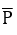
III. MỆNH ĐỀ KÉO THEO
Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, và kí hiệu là P => Q.
Mệnh đề P => Q còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
Mệnh đề P => Q chỉ sai khi P đúng và Q sai.
Như vậy, ta chỉ xét tính đúng sai của mệnh đề P => Q khi P đúng. Khi đó, nếu Q đúng thì P => Q đúng, nếu Q sai thì P => Q sai.
Các định lí, toán học là những mệnh đề đúng và thường có dạng P => Q.
Khi đó ta nói P là giả thiết, Q là kết luận của định lí, hoặc P là điều kiện đủ để có Q hoặc Q là điều kiện cần để có P.
IV. MỆNH ĐỀ ĐẢO – HAI MỆNH ĐỀ TƯƠNG ĐƯƠNG
Mệnh đề Q => P được gọi là mệnh đề đảo của mệnh đề P => Q
Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Nếu cả hai mệnh đề P => Q và Q => P đều đúng ta nói P và Q là hai mệnh đề tương đương. Khi đó ta có kí hiệu P Q và đọc là P tương đương Q, hoặc P là điều kiện cần và đủ để có Q, hoặc P khi và chỉ khi Q.
V. KÍ HIỆU ∀ VÀ ∃
Ví dụ: Câu “Bình phương của mọi số thực đều lớn hơn hoặc bằng 0” là một mệnh đề. Có thể viết mệnh đề này như sau
∀x ∈ R : x2 ≥ 0 hay x2 ≥ 0, ∀x ∈ R.
Kí hiệu ∀ đọc là “với mọi”.
Ví dụ: Câu “Có một số nguyên nhỏ hơn 0” là một mệnh đề
Có thể viết mệnh đề này như sau
∃n ∈ Z : n < 0.
Kí hiệu ∃ đọc là “có một” (tồn tại một) hay “có ít nhất một” (tồn tại ít nhất một).
Phủ định của mệnh đề “∀x ∈ X, P(x) ” là mệnh đề “ ∃x ∈ X, 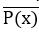
Phủ định của mệnh đề “∃x ∈ X, P(x)” là mệnh đề “ ∀ x ∈ X, 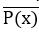


.jpg)
.jpg)

