I. Các tập hợp số

Mối quan hệ của các tập hợp số 

1. Tập các số tự nhiên 

2. Tập các số nguyên 

Tập hợp các số nguyên gồm các số tự nhiên và các số nguyên âm 

3. Tập hợp các số hữu tỉ 

- Các số hữu tỉ thường được biểu diễn dưới dạng 1 phân số , trong đó . Hai phân số  và  biểu diễn cùng một số hữu tỉ khi và chỉ khi .

Nói cách khác: 

- Số hữu tỉ còn được biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ: 

4. Tập hợp các số thực 

- Tập hợp các số thực gồm các số thập phân hữu hãn, vô hạn tuần hoàn và vô hạn không tuần hoàn. Các số thập phân vô hạn không tuần hoàn gọi là số vô tỉ.

- Tập hợp các số vô tỉ kí hiệu là I

- Tập hợp các số thực bao gồm các số hữu tỉ và các số vô tỉ.

II. Các tập hợp con thường dùng của 

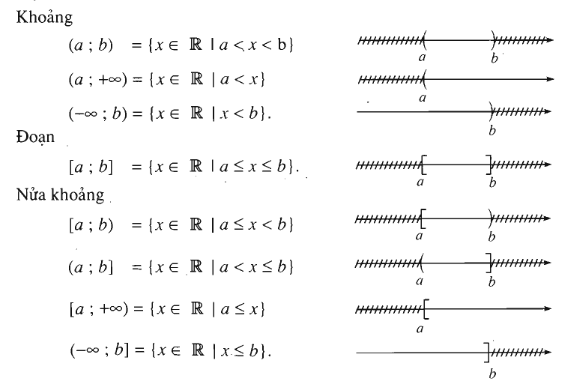
Kí hiệu:

 là dương vô cực (dương vô cùng)

 là âm vô cực (âm vô cùng)

 đồng nghĩa với mọi số thực x

Ví dụ: Xác định các tập hợp và biểu diễn chúng trên trục số:

a. 

b. 

Hướng dẫn giải