I. Khái niệm tập hợp

1. Tập hợp và phần tử

Ví dụ: Dùng kí hiệu  để viết các mệnh đề sau:

a. 4 là số tự nhiên

b. không là số hữu tỉ.

Hướng dẫn

a. 

b. 

- Tập hợp là khái niệm cơ bản của toán học, không có định nghĩa.

- Để nói a là một phần tử của tập hợp A, ta viết , ngược lại  để nói a không thuộc A

-Một tập hợp có thể được cho bằng cách liệt kê các phần tử của nó hoặc được cho bằng cách nêu tính chất đặc trưng của các phần tử của nó.

- Một phần tử không có phần tử nào được gọi là tập hợp rỗng, kí hiệu: 

2. Cách xác định tập hợp

Ta có thể xác định một tập hợp bằng 2 cách:

a. Liệt kê các phần tử của nó.

b. Chỉ ra tính chất đặc trưng cho các phần tử của nó.

Ví dụ: Cho tập hợp B là các nghiệm của phương trình  được viết là

Hãy liệt kê các phần tử có trong tập hợp.

Hướng dẫn

Các phần tử có trong tập hợp 

II. Tập hợp con

Ta gọi A là tập hợp con của B, kí hiệu 

Ví dụ:

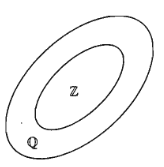
III. Tập hợp bằng nhau

Khi  và  ta nói tập hợp A bằng tập hợp B và viết là . Như vậy: