Đề kiểm tra Toán 12
Thời gian làm bài: 15 phút
Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số y = ax và đồ thị hàm số y =logaax đối xứng nhau qua đường thẳng y = x.
B. Hàm số y = ax với 0 < a < 1 đồng biến trên khoảng (-∞;+∞).
C. Hàm số y = ax với a > 1 nghịch biến trên khoảng (-∞;+∞).
D. Đồ thị hàm số y = ax với a > 0 và a ≠ 1 luôn đi qua điểm M(a; 1).
Câu 2. Cho hàm số 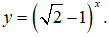
A. Hàm số nghịch biến trên khoảng (-∞;+∞).
B. Hàm số đồng biến trên khoảng (0;+∞).
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
Câu 3. Tập xác định của hàm số 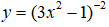
Câu 4. Tìm x để hàm số 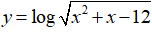
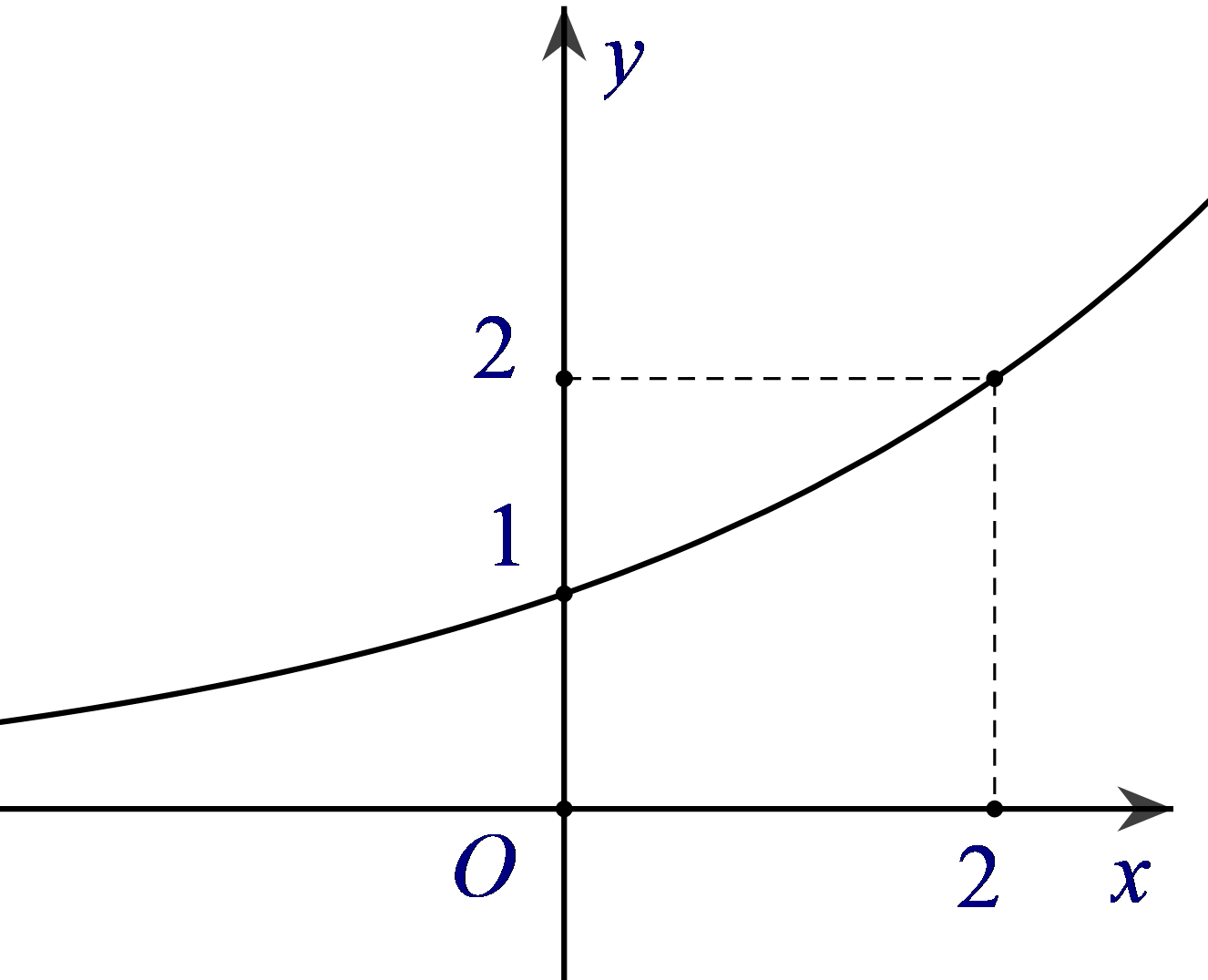
Câu 5. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 6. Hàm số 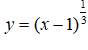
Câu 7. Đạo hàm của hàm số y = 42x là:
Câu 8. Đạo hàm của hàm số y = log5x, x > 0 là:
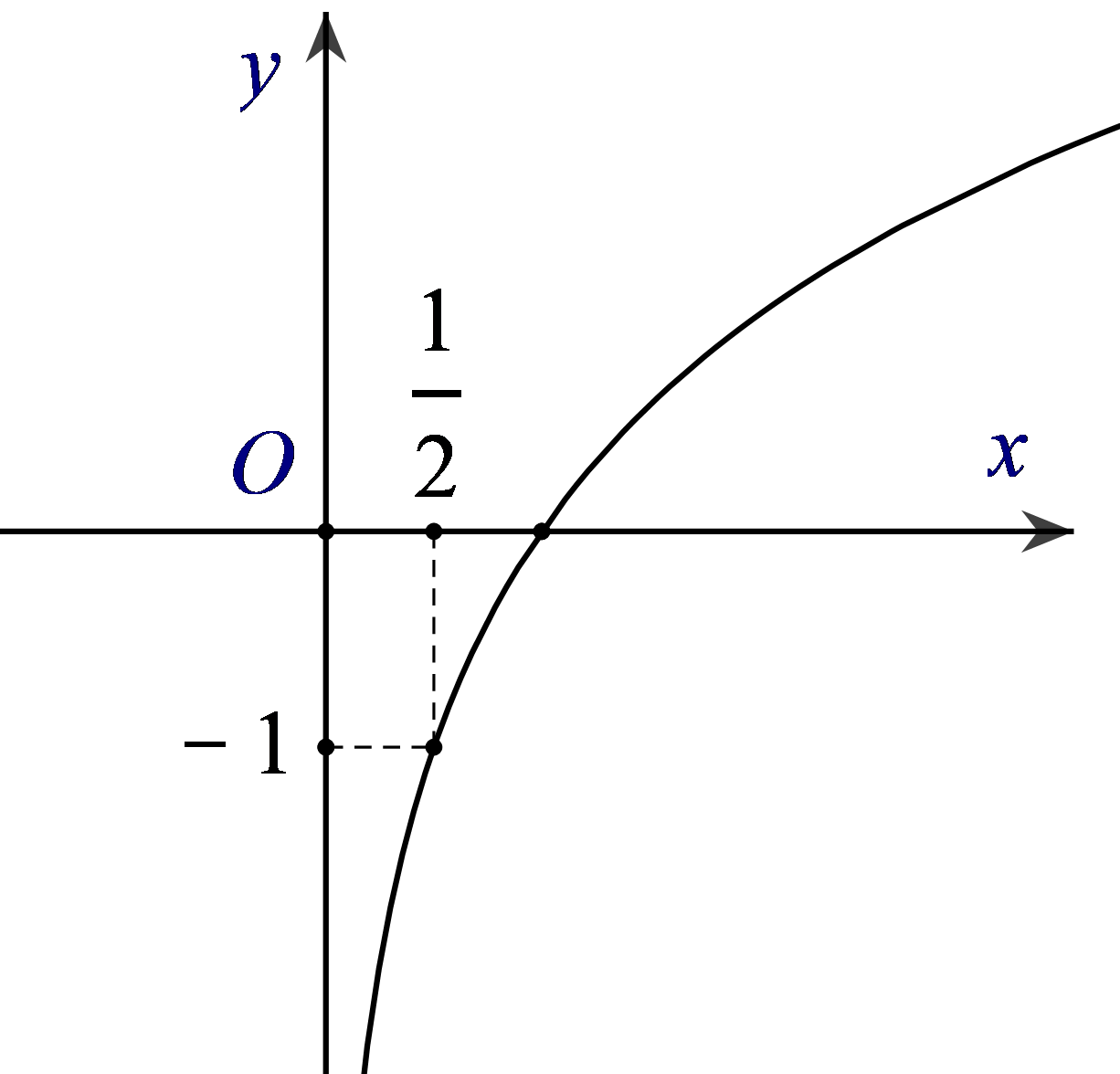
Câu 9. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
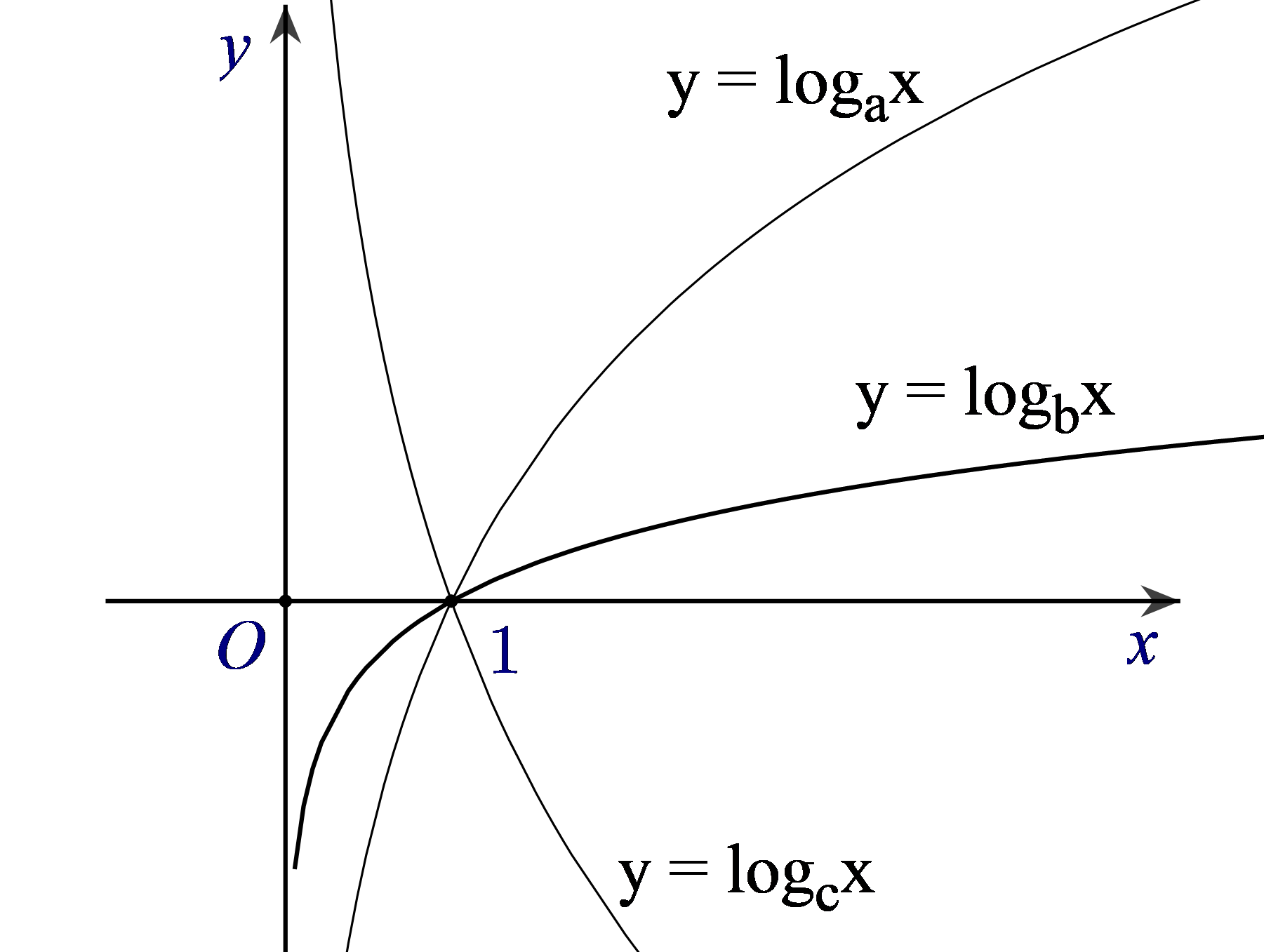
Câu 10. Hình bên là đồ thị của ba hàm số 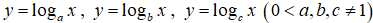
A. b > a > c
B. a > b > c
C. b > c > a
D. a > c > b
Đáp án & Hướng dẫn giải
Câu 1.
Chọn A
Câu B sai vì hàm số y = ax với 0 < a < 1 nghịch biến trên khoảng (-∞;+∞).
Câu C sai vì hàm số y = ax với a > 1 đồng biến trên khoảng (-∞;+∞).
Câu D sai vì đồ thị hàm số y = ax với a > 0 và luôn đi qua điểm M(0;1) chứ không phải M(a;1)
Câu 2.
Chọn A
TXĐ: D = R.
Vì 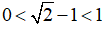
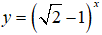
Câu 3.
Chọn B
Vì 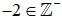
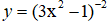
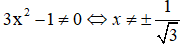
Câu 4.
Chọn C
Hàm số 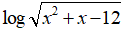
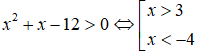
Câu 5.
Chọn A
Nhận thấy đây là đồ thị hàm số dạng y = ax. Hàm số đồng biến trên tập xác định.
Ta có điểm A(0;1) và B(2;2) thuộc đồ thị hàm số.
Câu 6.
Câu 7.
Chọn C
Câu 8.
Chọn A
Câu 9.
Chọn D.
Nhận thấy đây là đồ thị hàm số y = logax.
Điểm 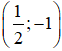
Câu 10.
Chọn A
Do y = logax và y = logbx là hai hàm đồng biến nên a > 1; b > 1
Do y = logcx nghịch biến nên c < 1 . Vậy c bé nhất.
Mặt khác: Lấy y = m, khi đó tồn tại x1; x2 > 0 để

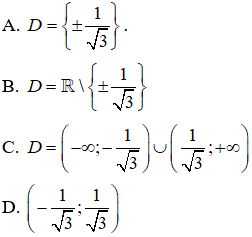
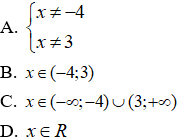
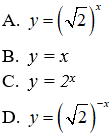
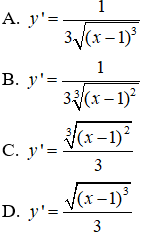
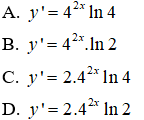
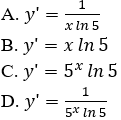
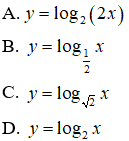
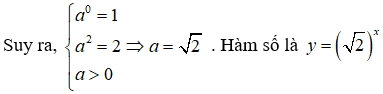
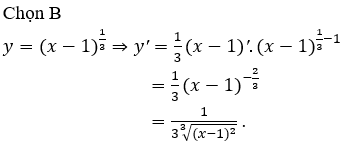
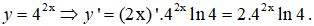
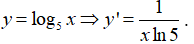
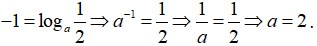
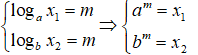
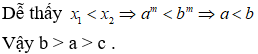

.jpg)
.jpg)

